

















In one of many greatest beefs in current hip-hop historical past, Drake and Kendrick Lamar are feuding — to the purpose that police had been requested...
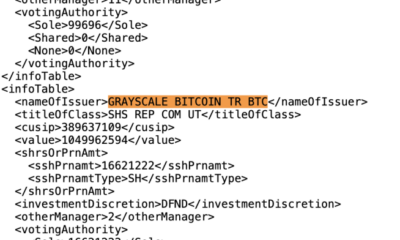

Susquehanna Worldwide Group, LLP (SIG), a world buying and selling, know-how, and funding agency, disclosed that it holds over $1.8 billion in Bitcoin exchange-traded funds (ETFs)...


Normal Hospital weekly predictions deal with Ava Jerome and Valentin Cassadine, Kristina Corinthos, Carly Corinthos Spencer and Valentin, Laura Spencer Collins, and Sam McCall, Jason Morgan...


Russia on Monday threatened to strike British navy services and stated it will maintain drills simulating the usage of battlefield nuclear weapons amid sharply rising tensions...
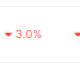
Pessimism surrounding Spot Ethereum ETFs approval is ready to extend as the USA Securities and Change Fee (SEC) has opted to delay its determination on the...


This week Jonathan is joined by Marc and Aron of The Disco Biscuits. They speak with Jonathan in regards to the origins of the band and...


In the course of the 2024 Met Gala purple carpet, Vogue world editorial director Anna Wintour stunned style followers when she walked the purple carpet in...


Ethereum (ETH), the world’s second-largest cryptocurrency, continues to grapple with uncertainty after a steep value decline. Buyers are on tenterhooks, with whales exiting their positions and...


Rihanna Steve Granitz/FilmMagic Nobody does the Met Gala like Rihanna — however this 12 months, a last-minute sickness stored her from taking a bow. Though the...


Even earlier than Chloe Fineman joined the forged of Saturday Evening Reside in 2019, she was dazzling her social media followers together with her superstar impression movies. Fineman’s Instagram continues...